Recovery from Deadlock

Recovery from Deadlock

There are three basic approaches to recovery from deadlock:

1. Inform the system operator, and allow him/her to take manual intervention.
2. Terminate one or more processes involved in the deadlock
3. Preempt resources.

Process Termination

Two basic approaches, both of which recover resources allocated to terminated processes:

• Terminate all processes involved in the deadlock. This definitely solves the deadlock, but at the expense of terminating more processes than would be absolutely necessary.
• Terminate processes one by one until the deadlock is broken. This is more conservative, but requires doing deadlock detection after each step.  In this case there are many factors that can go into deciding which processes to terminate next.

Resource Preemption

When preempting resources to relieve deadlock, there are three important issues to be addressed:

1. Selecting a victim - Deciding which resources to preempt from which processes involves many of the same decision criteria outlined above.
2. Rollback - Ideally one would like to roll back a preempted process to a safe state prior to the point at which that resource was originally allocated to the process. Unfortunately it can be difficult or impossible to determine what such a safe state is, and so the only safe rollback is to roll back all the way back to the beginning. ( I.e. abort the process and make it start over. )
3. Starvation - How do you guarantee that a process won't starve because its resources are constantly being preempted? One option would be to use a priority system, and increase the priority of a process every time its resources get preempted. Eventually it should get a high enough priority that it won't get preempted any more.

Deadlock Detection

Deadlock Detection

If a system does not employ either deadlock prevention or a deadlock avoidance algorithm, then a deadlock situation may occur. If deadlocks are not avoided, then another approach is to detect when they have occurred and recover somehow.

The system may provide:

1. An algorithm that examines the state of the system to determine whether a deadlock has occurred.

2. An algorithm to recover from the deadlock.

Single Instance of Each Resource Type

If each resource category has a single instance, then we can use a variation of the resource-allocation graph known as a wait-for graph.

A wait-for graph can be constructed from a resource-allocation graph by eliminating the resources and collapsing the associated edges, as shown in the figure below.An arc from Pi to Pj in a wait-for graph indicates that process Pi is waiting for a resource that process Pj is currently holding.

Several Instances of a Resource Type

Wait for graph is not applicable to a system with multiple instances of each resource type. The detection algorithm outlined here is essentially the same as the Banker's algorithm, with two subtle differences:

1. Let Work and Finish be vectors of length ‘m’ and ‘n’ respectively. Initialize Work=Available. For i=0,1,2,…..,n-1, if Allocation ≠ 0 then Finish[i] = false otherwise, Finish [i] = true.

2. Find an index i such that

            a. Finish[i] = = false

            b. Request­_i ≤ Work

If no such i exists, go to step 4

3. Set Work = Work + Allocation[ i ], and set Finish[ i ] to true. This corresponds to process i finishing up and releasing its resources back into the work pool. Then loop back to step 2.

4. If Finish[ i ] == true for all i, then there is no deadlock. This algorithm is more specific, by stating that if Finish[ i ] == false for any process Pi, then that process is specifically involved in the deadlock which has been detected.

Example:

Detection-Algorithm Usage

The answer to the question, when should detection algorithm must be invoked depends on two factors:

1. How often is a deadlock likely to occur?

2. How many processes will be affected by deadlock when it happens?

There are two obvious approaches, each with trade-offs:

1. Do deadlock detection after every resource allocation which cannot be immediately granted. This has the advantage of detecting the deadlock right away, while the minimum numbers of processes are involved in the deadlock. The down side of this approach is the extensive overhead and performance hit caused by checking for deadlocks so frequently.

2. Do deadlock detection only when there is some clue that a deadlock may have occurred, such as when CPU utilization reduces to 40% or some other magic number. The advantage is that deadlock detection is done much less frequently, but the down side is that it becomes impossible to detect the processes involved in the original deadlock, and so deadlock recovery can be more complicated and damaging to more processes.

Deadlock Avoidance

Deadlock Avoidance

The general idea behind deadlock avoidance is to prevent deadlocks from ever happening. This requires more information about each process, and tends to lead to low device utilization. In some algorithms the scheduler only needs to know the maximum number of each resource that a process might potentially use. When a scheduler sees that starting a process or granting resource requests may lead to future deadlocks, then that process is just not started or the request is not granted. A resource allocation state is defined by the number of available and allocated resources, and the maximum requirements of all processes in the system.

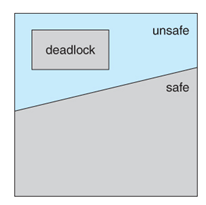
1. Safe State

A state is safe if the system can allocate all resources requested by all processes without entering a deadlock state. Formally, a state is safe if there exists a safe sequence of processes { P0, P1, P2, ..., PN } such that all of the resource requests for Pi can be granted using the resources currently allocated to Pi and all processes Pj where j < i.

If a safe sequence does not exist, then the system is in an unsafe state, which may lead to deadlock. All safe states are deadlock free, but not all unsafe states lead to deadlocks.

Example:

	Maximum Needs	Current Allocation
P0	10	5
P1	4	2
P2	9	2

Consider a system with 12 tape drives, allocated as above. Is this a safe state? What is the safe sequence?

The required are 9 (5+2+2), available are 3 (12-9). The system is in safe state. The sequence<P1,P0,P2> satisfies the safety condition. P1 can be allocated all resources and release all( available are 5) then P0 can be allocated and release(available 10) and finally P2(12 remaining).

2.  Resource-Allocation Graph algorithms

If resource categories have only single instances of their resources, then deadlock states can be detected by cycles in the resource-allocation graphs. Unsafe states can be recognized and avoided by adding to the resource-allocation graph with claim edges, noted by dashed lines, which point from a process to a resource that it may request in the future. A claim edge Pi → Rj indicates that a process Pi may request resource Rj in future.

When a process makes a request, the claim edge Pi->Rj is converted to a request edge. Similarly when a resource is released, the assignment reverts back to a claim edge. This approach works by denying requests that would produce cycles in the resource-allocation graph, taking claim edges into effect.

Example: Consider resource allocation graph

What happens when process P2 requests resource R2:

The resulting resource-allocation graph would have a cycle in it, and so the request cannot be granted.

3. Banker's Algorithm

For resource categories that contain more than one instance the resource-allocation graph method does not work, and more complex methods must be chosen. Banker’s algorithm is applicable to such system but less efficient.

The Banker's Algorithm gets its name because it is a method that bankers could use to assure that when they lend out resources they will still be able to satisfy all their clients.

When a process starts up, it must state in advance the maximum allocation of resources it may request, up to the amount available on the system. When a request is made, the scheduler determines whether granting the request would leave the system in a safe state. If not, then the process must wait until the request can be granted safely.

The banker's algorithm relies on several key data structures: ( where n is the number of processes and m is the number of resource categories. )

• Available[ m ] indicates how many resources are currently available of each type.
• Max[ n ][ m ] indicates the maximum demand of each process of each resource.
• Allocation[ n ][ m ] indicates the number of each resource category allocated to each process.
• Need[ n ][ m ] indicates the remaining resources needed of each type for each process. ( Note that Need[ i ][ j ] = Max[ i ][ j ] - Allocation[ i ][ j ] for all i, j. )

a. Safety Algorithm

In order to apply the Banker's algorithm, we first need an algorithm for determining whether or not a particular state is safe. This algorithm determines if the current state of a system is safe, according to the following steps:

1. Let Work and Finish be vectors of length m and n respectively.
• Work is a working copy of the available resources, which will be modified during the analysis.
• Finish is a vector of booleans indicating whether a particular process can finish. ( or has finished so far in the analysis. )
• Initialize Work to Available, and Finish to false for all elements.
2. Find an i such that both

(A) Finish[ i ] == false, and

(B) Need[ i ] < Work.

If no such i exists, go to step 4.

3. Set Work = Work + Allocation[ i ], and set Finish[ i ] to true. This corresponds to process i finishing up and releasing its resources back into the work pool. Then loop back to step 2.
4. If finish[ i ] == true for all i, then the state is a safe state, because a safe sequence has been found.

b. Resource Request algorithm (Banker’s algorithm)

This algorithm determines if a new request is safe, and grants it only if it is safe to do so. When a request is made ( that does not exceed currently available resources ), pretend it has been granted, and then see if the resulting state is a safe one.

If so, grant the request, and if not, deny the request, as follows:

1.        Let Request[ n ][ m ] indicate the number of resources of each type currently requested by processes. If Request[ i ] > Need[ i ] for any process i, raise an error condition.

2.        If Request[ i ] > Available for any process i, then that process must wait for resources to become available. Otherwise the process can continue to step 3.

3.        Check to see if the request can be granted safely, by pretending it has been granted and then seeing if the resulting state is safe. If so, grant the request, and if not, then the process must wait until its request can be granted safely. The procedure for granting a request ( or pretending to for testing purposes ) is:

• Available = Available - Request
• Allocation = Allocation + Request
• Need = Need - Request

Deadlock Prevention

Deadlock Prevention

Deadlocks can be prevented by preventing at least one of the four required conditions:

Mutual Exclusion

• Shared resources such as read-only files do not lead to deadlocks.
• Unfortunately some resources, such as printers and tape drives, require exclusive access by a single process.

 Hold and Wait

• To prevent this condition processes must be prevented from holding one or more resources while simultaneously waiting for one or more others. There are several possibilities for this:
• Require that all processes request all resources at one time. This can be wasteful of system resources if a process needs one resource early in its execution and doesn't need some other resource until much later.
• Require that processes holding resources must release them before requesting new resources, and then re-acquire the released resources along with the new ones in a single new request. This can be a problem if a process has partially completed an operation using a resource and then fails to get it re-allocated after releasing it.
• Either of the methods described above can lead to starvation if a process requires one or more popular resources.

No Preemption

• Preemption of process resource allocations can prevent this condition of deadlocks, when it is possible.
• One approach is that if a process is forced to wait when requesting a new resource, then all other resources previously held by this process are implicitly released, ( preempted ), forcing this process to re-acquire the old resources along with the new resources in a single request, similar to the previous discussion.
• Another approach is that when a resource is requested and not available, then the system looks to see what other processes currently have those resources and are themselves blocked waiting for some other resource. If such a process is found, then some of their resources may get preempted and added to the list of resources for which the process is waiting.
• Either of these approaches may be applicable for resources whose states are easily saved and restored, such as registers and memory, but are generally not applicable to other devices such as printers and tape drives.

Circular Wait

• One way to avoid circular wait is to number all resources, and to require that processes request resources only in strictly increasing ( or decreasing ) order. In other words, in order to request resource Rj, a process must first release all Ri such that i >= j.
• One big challenge in this scheme is determining the relative ordering of the different resources

Deadlocks

Deadlocks

In a multi programming environment several processes may compete for finite number of resources.

In normal operation a process must request a resource before using it, and release it when it is done, in the following sequence:

1. Request - If the request cannot be immediately granted, then the process must wait until the resource(s) it needs become available. For example the system calls open( ), malloc( ), new( ), and request( ).
2. Use - The process uses the resource, e.g. prints to the printer or reads from the file.
3. Release - The process relinquishes the resource. so that it becomes available for other processes. For example, close( ), free( ), delete( ), and release( ).

A set of processes is deadlocked when every process in the set is waiting for a resource that is currently allocated to another process in the set ( and which can only be released when that other waiting process makes progress. )

Deadlock Characterization

1. Necessary Conditions

There are four conditions that are necessary for a deadlock:

1. Mutual Exclusion - At least one resource must be held in a non-sharable mode; If any other process requests this resource, then that process must wait for the resource to be released. (Only one process at a time can use the resource)
2. Hold and Wait - A process must be simultaneously holding at least one resource and waiting for at least one resource that is currently being held by some other process.
3. No preemption - Once a process is holding a resource ( i.e. once its request has been granted ), then that resource cannot be taken away from that process until the process voluntarily releases it.
4. Circular Wait - A set of processes { P0, P1, P2, . . ., PN } must exist such that every P[ i ] is waiting for P[ ( i + 1 ) % ( N + 1 ) ]. (Hold and wait)

2. Resource Allocation Graph

Deadlocks can be understood more clearly through the use of Resource-Allocation Graphs, having the following properties

• A set of resource categories, { R1, R2, R3, . . ., RN }, which appear as square nodes on the graph. Dots inside the resource nodes indicate specific instances of the resource.
• A set of processes, { P1, P2, P3, . . ., PN }
• Request Edges - A set of directed arcs from Pi to Rj, indicating that process Pi has requested Rj, and is currently waiting for that resource to become available.
• Assignment Edges - A set of directed arcs from Rj to Pi indicating that resource Rj has been allocated to process Pi, and that Pi is currently holding resource Rj.

• If a resource-allocation graph contains no cycles, then the system is not deadlocked.
• If a resource-allocation graph does contain cycles AND each resource category contains only a single instance, then a deadlock exists.
• If a resource category contains more than one instance, then the presence of a cycle in the resource-allocation graph indicates the possibility of a deadlock, but does not guarantee one.

Methods for Handling Deadlocks

Generally there are three ways to handle Deadlocks:

1. Deadlock prevention or avoidance - Do not allow the system to get into a deadlocked state.
2. Deadlock detection and recovery - Abort a process or preempt some resources when deadlocks are detected.
3. Ignore the problem all together - This is the approach that both Windows and UNIX take. Pretends that deadlocks never occur. 

If deadlocks are neither prevented nor detected, then when a deadlock occurs the system will gradually slow down, as more and more processes become stuck waiting for resources currently held by the deadlock and by other waiting processes. 

Monitors

Semaphores can be very useful for solving concurrency problems, but only if programmers use them properly. If even one process fails to abide by the proper use of semaphores, either accidentally or deliberately, then the whole system breaks down. For this reason a higher-level language construct has been developed, called monitors.

Monitor Usage

• A monitor is essentially a class, in which all data is private, and with the special restriction that only one method within any given monitor object may be active at the same time. An additional restriction is that monitor methods may only access the shared data within the monitor and any data passed to them as parameters. i.e. they cannot access any data external to the monitor.

In order to fully realize the potential of monitors, one additional new data type, known as a condition can be defined.

• A variable of type condition has only two legal operations, wait and signal. i.e. if X was defined as type condition, then legal operations would be X.wait( ) and X.signal( )
• The wait operation blocks a process until some other process calls signal, and adds the blocked process onto a list associated with that condition.
• The signal process does nothing if there are no processes waiting on that condition. Otherwise it wakes up exactly one process from the condition's list of waiting processes.

·           But now there is a potential problem - If process P within the monitor issues a signal that would wake up process Q also within the monitor, then there would be two processes running simultaneously within the monitor, violating the exclusion requirement.

·           Accordingly there are two possible solutions to this dilemma:

Signal and wait - When process P issues the signal to wake up process Q, P then waits, either for Q to leave the monitor or on some other condition.

Signal and continue - When P issues the signal, Q waits, either for P to exit the monitor or for some other condition.

Classic Problems of Synchronization

1. The Bounded-Buffer Problem

• This is a generalization of the producer-consumer problem wherein access is controlled to a shared group of buffers of a limited size.
• In this solution, the two counting semaphores "full" and "empty" keep track of the current number of full and empty buffers respectively ( and initialized to 0 and N respectively. ) The binary semaphore mutex controls access to the critical section. The producer and consumer processes are nearly identical - One can think of the producer as producing full buffers, and the consumer producing empty buffers.

2. The Readers-Writers Problem

• In the readers-writers problem there are some processes ( termed readers ) who only read the shared data, and never change it, and there are other processes ( termed writers ) who may change the data in addition to or instead of reading it. There is no limit to how many readers can access the data simultaneously, but when a writer accesses the data, it needs exclusive access.
• There are several variations to the readers-writers problem, most centered around relative priorities of readers versus writers.
• The first readers-writers problem gives priority to readers. In this problem, if a reader wants access to the data, and there is not already a writer accessing it, then access is granted to the reader. A solution to this problem can lead to starvation of the writers, as there could always be more readers coming along to access the data. ( A steady stream of readers will jump ahead of waiting writers as long as there is currently already another reader accessing the data, because the writer is forced to wait until the data is idle, which may never happen if there are enough readers. )
• The second readers-writers problem gives priority to the writers. In this problem, when a writer wants access to the data it jumps to the head of the queue - All waiting readers are blocked, and the writer gets access to the data as soon as it becomes available. In this solution the readers may be starved by a steady stream of writers.
• The following code is an example of the first readers-writers problem, and involves an important counter and two binary semaphores:
• readcount is used by the reader processes, to count the number of readers currently accessing the data.
• mutex is a semaphore used only by the readers for controlled access to readcount.
• rw_mutex is a semaphore used to block and release the writers. The first reader to access the data will set this lock and the last reader to exit will release it; The remaining readers do not touch rw_mutex. ( Eighth edition called this variable wrt. )

Note that the first reader to come along will block on rw_mutex if there is currently a writer accessing the data, and that all following readers will only block on mutex for their turn to increment readcount.

3. The Dining-Philosophers Problem

• The dining philosophers problem is a classic synchronization problem involving the allocation of limited resources amongst a group of processes in a deadlock-free and starvation-free manner:
• Consider five philosophers sitting around a table, in which there are five chopsticks evenly distributed and an endless bowl of rice in the center, as shown in the diagram below. ( There is exactly one chopstick between each pair of dining philosophers. )
• These philosophers spend their lives alternating between two activities: eating and thinking.
• When it is time for a philosopher to eat, it must first acquire two chopsticks - one from their left and one from their right.
• When a philosopher thinks, it puts down both chopsticks in their original locations.

• One possible solution, as shown in the following code section, is to use a set of five semaphores ( chopsticks[ 5 ] ), and to have each hungry philosopher first wait on their left chopstick ( chopsticks[ i ] ), and then wait on their right chopstick ( chopsticks[ ( i + 1 ) % 5 ] )
• But suppose that all five philosophers get hungry at the same time, and each starts by picking up their left chopstick. They then look for their right chopstick, but because it is unavailable, they wait for it, forever, and eventually all the philosophers starve due to the resulting deadlock.

Some potential solutions to the problem include:

• Only allow four philosophers to dine at the same time. ( Limited simultaneous processes. )
• Allow philosophers to pick up chopsticks only when both are available, in a critical section. ( All or nothing allocation of critical resources. )
• Use an asymmetric solution, in which odd philosophers pick up their left chopstick first and even philosophers pick up their right chopstick first. ( Will this solution always work? What if there are an even number of philosophers? )